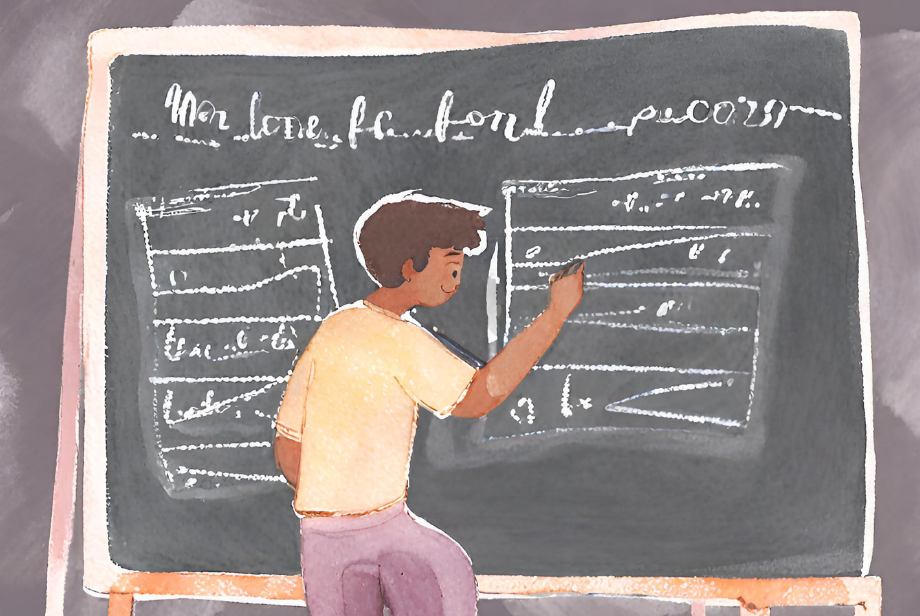During the spring of 2023, Applied Mathematics major Md Almasrafi (‘24) discovered what would become his “obsession” in his Number Theory class. Following the lesson, Almasrafi sought to uncover a new proof of the recursive equation for the sums of a sequence involving powers. Very few students find original proofs independently, but the proof of one complicated equation would unfold in Almasrafi’s dream and become the topic of his research paper.
As he relentlessly solved math problems in class, Almasrafi cracked the explicit formula for partial sums independently. In combinatorics, an area of math focused on counting, this formula aims to solve the sum of powers from any value in a data set.
Mr. Scott Matthews, a Math Research and Number Theory teacher, explained that “1 + 4 + 9 + 16 is a partial sum of a sequence of perfect squares.” An easier approach to finding the partial sum of a long sequence would be applying this formula rather than deriving the answer by hand.
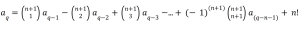
The formula can help extrapolate data in Physics and other fields. “Let’s say you have a set of data and you only collected it to a certain point,” Almasrafi explained. “You want to know what’s next but you only have experimental data. You could just plug it into this equation.”
Initially, Almasrafi did not recognize the explicit equation because his teacher had yet to present it to the class. “[The explicit formula] was a self-discovery, but later on, I found out that it already existed,” he explained.
While Almasrafi did not create a new formula, his deep, new-found interest in discrete mathematics, specifically recursive functions, inspired weeks of hunting for the elusive proof in his Math Research class.
Rather than finding the proof for the explicit formula, he had proven the recursive formula, which finds any number by relying on the previous term in a sequence. He approached his proof by finding the common differences. Almasrafi explained that this technique is successful because there will always be a common difference in a polynomial sequence.
Although he successfully proved the general recursive formula, he faced many challenges. “The challenges faced were very analytical,” explained Almasrafi. As shown in the picture below, he had to prove proofs one through seven to develop his overall proof. For example, proof seven, otherwise known as the end factorial, was a challenging proof he had to incorporate into his overall proof.
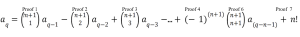
The research required extensive effort and time. “I spent my entire spring break on it,” Almasrafi admitted. Over that break, he went to the library five hours per day to finish his proof. It was then he encountered his main obstacle. “As spring break was about to end, I was stuck on this end factorial,” he explained.
Amazingly, the solution came to him in a dream. “It was the day before we were supposed to come back, I woke up at 3 A.M. and was like I figured it out! I woke up, wrote it, and went back to sleep,” Almasrafi remembered.
Throughout the spring semester, he sought guidance from Mr. Matthews and his friend and fellow Applied Mathematics major, Lucas Papamitsakis (‘24).
At the time, Almasrafi had not taken AP Calculus, so Papamitsakis answered questions concerning that field. “I was telling him how these different calculus rules work like integration and derivatives,” stated Papamitsakis. “That’s sort of how he realized he could use recursions to emulate that. It was interesting how he could combine discrete math and calculus.”
Matthews was impressed. “All of the students worked hard on their Math Research Papers, and Md dove in and put in more hours than is typical,” he said. “He felt extremely compelled to find answers to his questions, and it was exciting to see the nice results of his hard work.”
Almasrafi acknowledged that the formula only works with rational and positive x values. However, he explained that “there is definitely more to expand on this equation.”
He believes this research is only the beginning of his career aspirations. “Hypothetically, in eight years when I’m doing my master’s in math and I have to write a thesis, I could write a thesis on this.”
Amasrafi hopes other students will follow his lead. For those who are interested in exploring their own research topics, Almasrafi counsels that success lies in their curiosity and drive. “The research paper may be scary, but all it requires is a little passion,” he explained. “A lot of times you’re taught the equation but you’re not sure how it works because a lot of times they just don’t educate you onto that level. Just explore it yourself.”